Camera Calibration and 3D Reconstruction

Source: opencv

In camera calibration I presented how to call the camera_calibration ROS package to calibrate a pinhole camera (in my case). Now I want to understand the mathematics behind it. It looks a lot like the mathematics applied in camera backward projection.

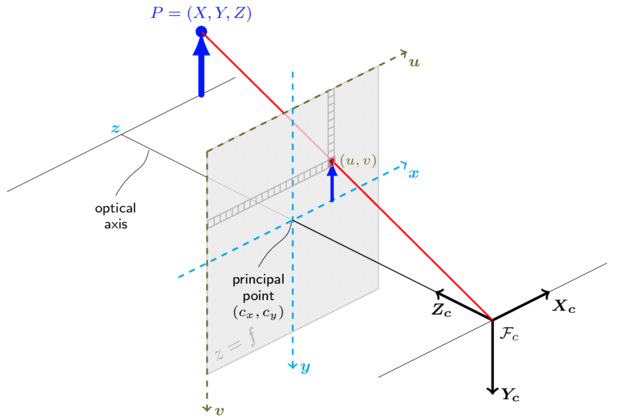
For pinhole camera model, a scene is formed by projecting 3D points into the image plane using a perspective transformation:

$$s\cdot {\mathbf{m}}^{\prime }=\mathbf{A}\left[\begin{array}{c}\mathbf{R}|\mathbf{t}\end{array}\right]{\mathbf{M}}^{\prime }$$

or

$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t_3\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$

where:

• $(X,Y,Z)$ are the coordinates of a 3D point in the world coordinate space
• $(u,v)$ are the coordinates of the projection point in pixels
• $\mathbf{A}$ is a camera matrix, or a matrix of intrinsic parameters
• $(c_x,c_y)$ is a principal point that is usually at the image center
• $f_x,f_y$ are the focal lengths expressed in pixel units.

Tip

If an image from the camera is scaled by a factor, all of these params should be scaled by the same factor! However, the intrinsic parameters do not depend on the scene viewed, so as long as the focal length is fixed, they can be re-used.

Similar to camera backward projection, the joint rotation of R and t describe the camera motion around a static scene (as litter is usually stationary in the ocean, as in on the bottom) and it translates coordinates of a point $(X,Y,Z)$ to a coordinate system, fixed with respect to the camera. When $z\ne 0$:

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\mathbf{R}\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]+\mathbf{t}$$ $$x^{\prime }=\frac{x}{z}$$ $$y^{\prime }=\frac{y}{z}$$ $$u=f_x\cdot x^{\prime }+c_x$$ $$v=f_y\cdot y^{\prime }+c_y$$

As lenses usually present distortion, the above model is extended as:

$$x^{\prime \prime }=x^{\prime }\frac{1+k_1{r}^2+k_2{r}^4+k_3{r}^6}{1+k_4{r}^2+k_5{r}^4+k_6{r}^6}+2p_1{x}^{\prime }{y}^{\prime }+p_2(r^2+2x^{\prime 2})$$ $$y^{\prime \prime }=y^{\prime }\frac{1+k_1{r}^2+k_2{r}^4+k_3{r}^6}{1+k_4{r}^2+k_5{r}^4+k_6{r}^6}+p_1(r^2+2y^{\prime 2})+2p_2{x}^{\prime }{y}^{\prime }$$

where,

$$r^2=x^{\prime 2}+y^{\prime 2}$$ $$u=f_x\cdot x^{\prime \prime }+c_x$$ $$v=f_y\cdot y^{\prime \prime }+c_y$$

The distortion vector contains $(k_1,k_2,p_1,p_2)$, where $k_1$ and $k_2$ are radial distortion coefficients and $p_1$ and $p_2$ are tangential distortion coefficients.

Distortion coefficients are also intrinsic parameters

If a camera has been calibrated for images of $320\times 240$, the same distortion coefficients can be used for $640\times 480$ images from the same camera while $f_x,f_y,c_x$ and $c_y$ need to be scaled appropriately.

I did something similar to this in my visual-odom implementation without the need to explicit the camera intrinsic parameters and I would deduce matrix $\mathbf{A}=\left[\begin{array}{c}\mathbf{R}|\mathbf{t}\end{array}\right]$ based on affine transformations.