Camera Backward Projection

Backward camera projection maps points from a 2D image plane (captured by a camera) back into the 3D world space

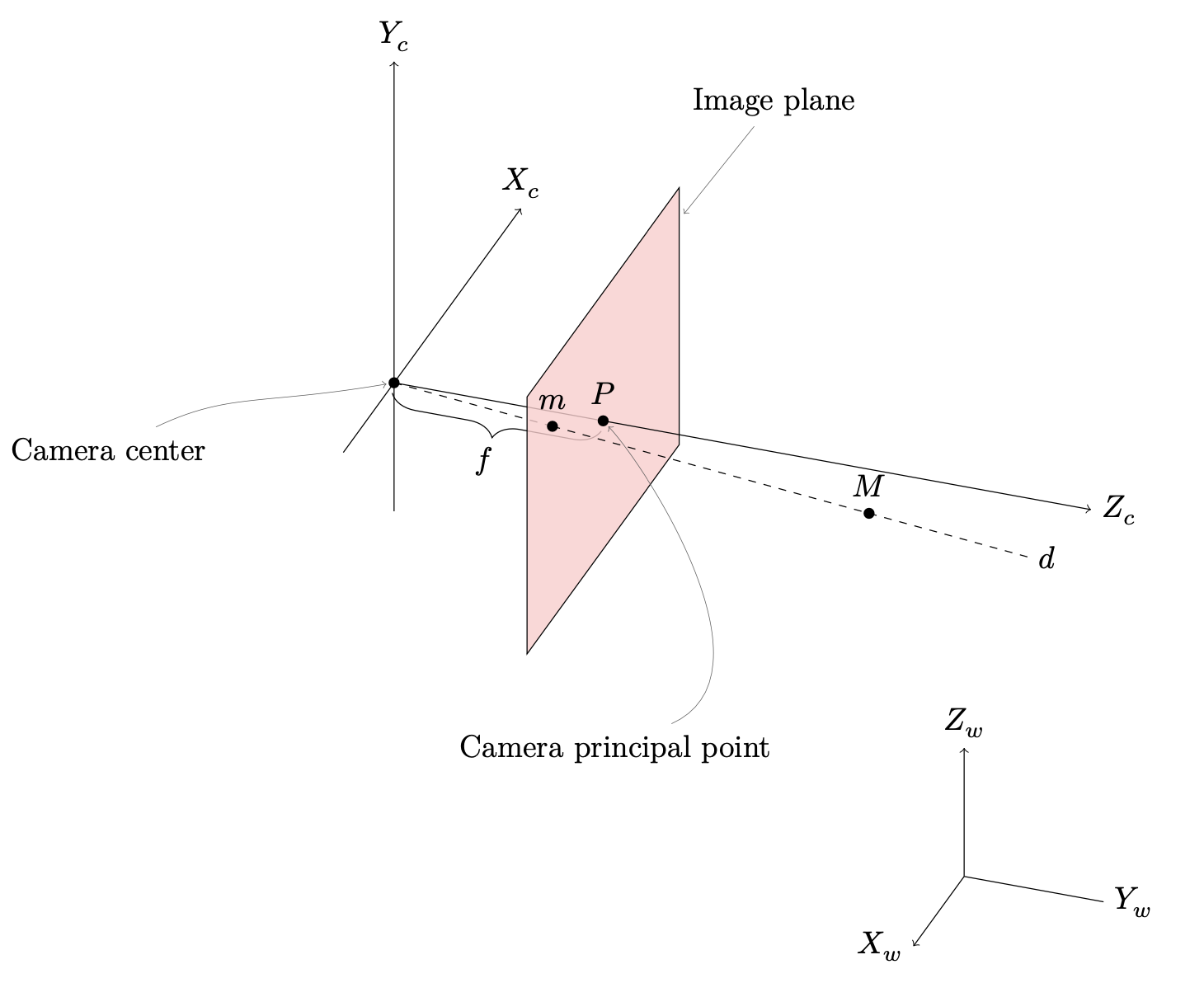
Above is presented the pinhole camera model. The image plane coordinates of the projection m of a point, represented in homogenous world coordinates, $M_w=\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]$ can be obtained from the equation below. $X_C,Y_C,Z_C$ axes describe the camera reference frame and the $X_W,Y_W,Z_W$ axes represent the world reference frame.

$$m=\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=KT{M}_w$$

where 𝑇 is the transformation between the word reference frame and the camera reference frame, and 𝐾 is the camera intrinsic matrix. The transformation matrix is a 4×4 rotation and translation matrix.

$$K=\left[\begin{array}{cccc}{\alpha }_x& 0& x_P& 0\\ 0& {\alpha }_y& y_P& 0\\ 0& 0& 1& 0\end{array}\right]$$

For a CCD camera, the intrinsic matrix has the above general form, where ${\alpha }_x$ and ${\alpha }_y$ represent the focal distance 𝑓 expressed in pixel dimensions along the two axes and the $(x_P,y_P)$ pair represent the image plane coordinates of the principal point, also expressed in pixel dimensions.

Due to the projective transformation, given a point in the image, we cannot determine the one point that has produced it, but only a ray on which the original point is found. This is also apparent in First Figure as any point on ray $d$ would have produced the same projected point in the image plane. Thus, in order to find the coordinates of a point $M_w$ more information is needed. For example, if it were known that the original point is found on a certain plane, the intersection between the line on which the point is found and said plane will yield the original point.

I have a code that detects and ArUco marker and draws the axis coordinates on the image through rosrun rqt_image_view rqt_image_view /colordetection. Also, by using the presented algorithm, I can detect it’s real-life coordinates.