Regression in Machine Learning

Regression is just like classification except the response variable is continuous.

Here are some examples of real-word regression problems.

• Predict tomorrow’s stock market price given current market conditions and other possible side information,
• Predict age of a viewer watching a given video on youtube,
• Predict the location in 3D space of a robot arm end effector, given control signals (torques) sent to its various motors,
• Predict the amount of prostate specific antigen (PSA) in the body as a function of a number of different clinical measurements,
• Predict the temperature at any location inside a building using weather data, time, door sensors, etc.

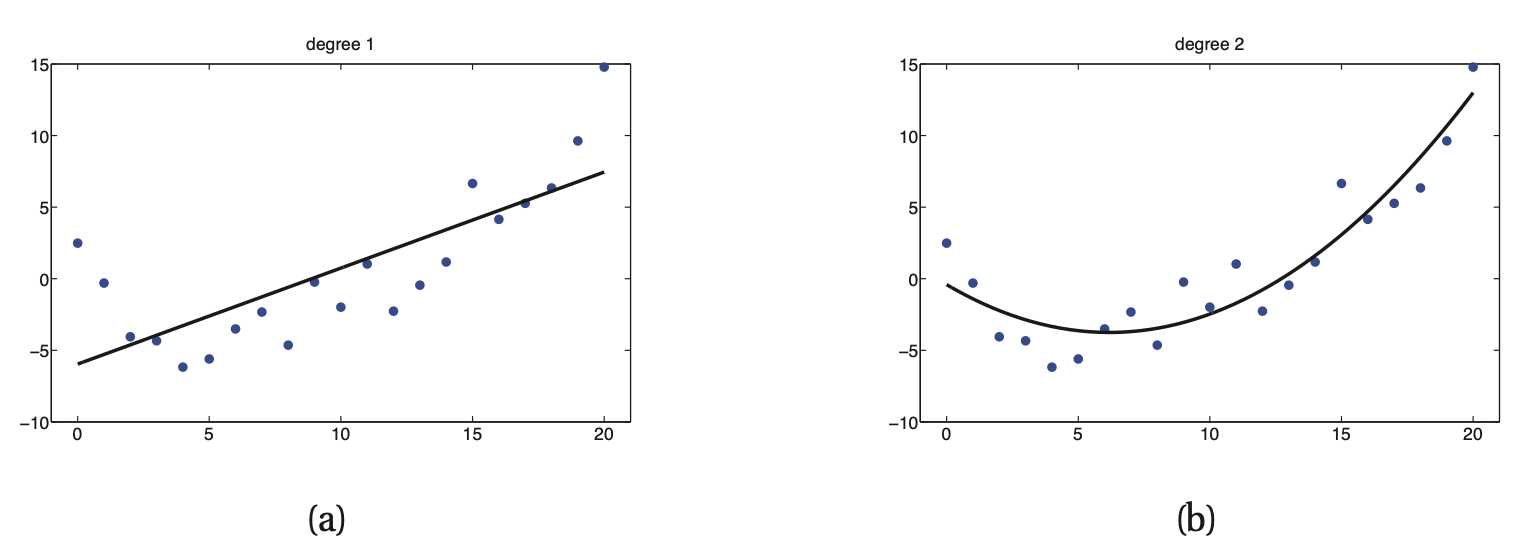
Linear Regression

Widely used. This asserts that the response is a linear function of the inputs.

$$y(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+ϵ=\sum _{j=1}^D{w}_j{x}_j+ϵ$$

,where:

• ${\mathbf{w}}^T\mathbf{x}$ represents the inner or scalar product between the input vector $\mathbf{x}$ and the model’s weight vector $\mathbf{w}$, and $ϵ$ is the residual error between our linear predictions and the true response.

We often assume that $ϵ$ has a Gaussian or normal distribution. So we can rewrite the model in the following form:

$$p(y|\mathbf{x},\mathbf{\theta })=\mathcal{N}(y|\mu (\mathbf{x}),{\sigma }^2(\mathbf{x}))$$

In the simplest case, we assume that $\mu$ is a linear function of $\mathbf{x}$, so $\mu ={\mathbf{w}}^T\mathbf{x}$, and that the noise is fixed, ${\sigma }^2(\mathbf{x})={\sigma }^2$. In this case, $\theta =(\mathbf{w},{\sigma }^2)$ are the params of the model.

For example, suppose the input is 1 dimensional. We can represent the expected response as follows:

$$\mu (x)=w_0+w_{1}x={\mathbf{w}}^T\mathbf{x}$$

,where $w_0$ is the intercept or bias term, $w_1$ is the slope, and where we have defined the vector $\mathbf{x}=(1,x)$.