Shunting Yard Algorithm

https://brilliant.org/wiki/shunting-yard-algorithm/ — source

I will apply this in order to parse a mathematical expression in C++. For example, $f(x)=6\ast x^4+3\ast x^2-sin(x+1)$. I want to pass this function further to optimization algorithms. I will need to look into computing the derivatives, jacobians and hessians (most likely with Eigen).

Apparently the way we write mathematical expressions is infix notation - Operators have precedence and brackets override this precedence.

The shunting yard algorithm assigns each operator it's correct operands, taking into account the order of the precedence.

Let’s take for example the following infix notation: $4+18/(9+3)$ The shunting yard will output the reverse polish notation as

$4,18,9,3,-,/,+$

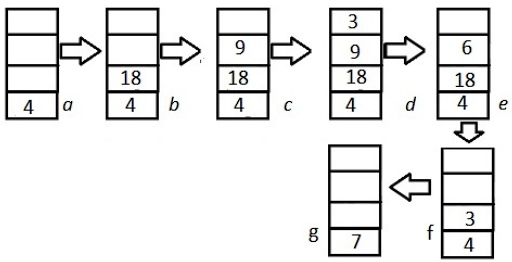
In steps a to d, it pushes the numbers in reverse polish ecpression into the stack. In step e, where the - operator has been reached, the two numbers are popped and push 9-3=6 back into the stack. The next operator would be / where it pops the 6 and 18 and performs the operation 18/6=3 and pushes it to the stack. The final procedure leaves 7.

To implement the algorithm, we need

• 1 stack for operations,
• 1 queue for the output,
• 1 array of tokens.

This is what a pseudocode version of this algorithm looks like:

  While there are tokens to be read:
        Read a token
        If it's a number add it to queue
        If it's an operator
               While there's an operator on the top of the stack with greater precedence:
                       Pop operators from the stack onto the output queue
               Push the current operator onto the stack
        If it's a left bracket push it onto the stack
        If it's a right bracket 
            While there's not a left bracket at the top of the stack:
                     Pop operators from the stack onto the output queue.
             Pop the left bracket from the stack and discard it
 While there are operators on the stack, pop them to the queue